コミュニケーション
ビジネスやプライベートで使える○○の法則100選

スポンサーリンク
ビジネスやプライベートで応用できる心理学や自然現象など○○の法則一覧
世の中には心理学に基づいた「希少性の法則」や「決定回避の法則」、統計によって導き出された「ベンフォードの法則」や「大数の法則」など様々な法則が存在しています。
それらの法則の全てが正しいとは限りませんが、中にはビジネスやプライベートにも活用できる法則もあります。
ここでは少し面白い法則やビジネスやプライベートにも活用できそうな法則を一覧にまとめてご紹介していきます。
パレートの法則(80対20の法則・ばらつきの法則)
「80対20の法則」や「ばらつきの法則」などとも呼ばれているパレードの法則とは、例えば会社全体の売上の内80%の売上を生み出しているは上位20%の商品であると言った法則です。
また他にも、1人の社員が出した成果の内の80%は、業務時間の20%によって生み出されている、○○税の80%は上位20%の富裕層が支払っていると言ったことで、様々な物事が80対20といった割合になるといった法則です。
パレードの法則は経済学者であり社会学者であるヴィルフレドパレート氏によって提唱された法則です。
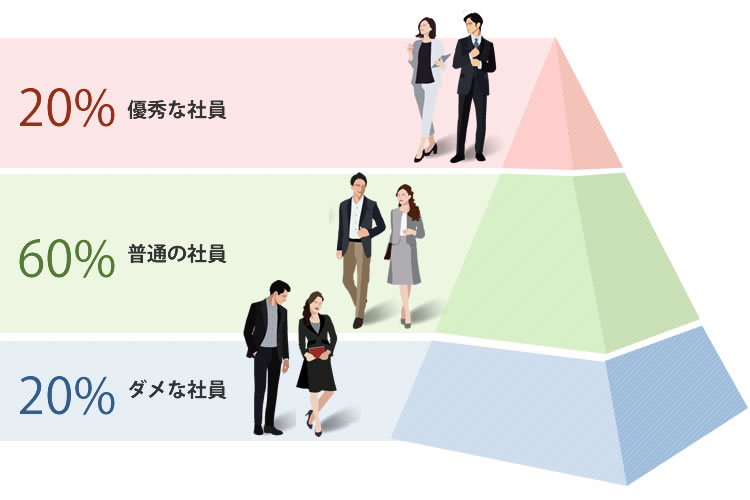
2対6対2の法則(働きアリの法則)
2対6対2の法則とは「様々な物事を3つのグループに分けると割合が2対6対2になる」と言った法則のことです。
例えば、従業員が100人の会社で「優秀な社員」「普通の社員」「ダメな社員」の3つに分けると優秀社員が20人、普通の社員が60人、ダメな社員が20人と言った割合なるといった具合です。
2対6対2の法則の面白いのは優秀な社員だけを集めた特別チームを作ったとしても時間が経つにつれて一部の社員が徐々に怠け始め2対6対2の法則の通りになると言われており、スター選手を多く集められるプロチームでも毎年優勝できないのはこの法則によるものだと言われています。
働きアリなどでも同じような現象が見られることから働きアリの法則とも呼ばれ、上記で紹介したパレードの法則の法則から派生した法則と言われています。
78対22の法則(ユダヤの法則)
78対22の法則とは「様々な要素が78対22の割合で構成され存在している」と言ったものです。
大気:78%の大気と22%の酸素や二酸化炭素などその他の物質で構成
地球:78%の海と22%の陸地で構成
人体:78%の水分と22%のその他の成分で構成
正方形と円:正方形の中に円をいっぱいに書くと円の面接が78%、四隅の合計面接が22%となる
と言ったように自然現象の中には78対22の法則が成り立つものが多く存在しています。
そのため最初に紹介したパレートの法則(80対20の法則)もこの法則によって成り立っているのかもしれません。
3の法則
3の法則とは
人は呼吸ができなければ約3分程度しか生きられない
人は全血液量の3分の1を失うと生命の危険にさらされる
人は食料も水分も全く取らない状況下では3日程度しか生きられない。
人は水分だけでは3週刊程度しか生きられない
と言った法則のことです。
ジラートの法則(ジラード250の法則)
ジラートの法則とは「1人の人はおおよそ250人の人とつながっている」と言った法則です。
つまり、ジラートの法則に従えば、1人の人を敵にまわすと言うことは250人の人を敵にまわすと言うことになります。
1.01と0.99の法則
1.01と0.99の法則とは1.01を365乗(365日)すると37.8となり、0.99を365乗すると0.03となることから「日々の積み重ね(日々の努力)が大切」と言った法則です。
1を基準に毎日ほんの少し(0.1)努力を続けるか、ほんの少しだらけるかで1年後には大きな力の差が生まれてしまいます。
3対33の法則
3対33の法則とは「サービスや物などに満足した人は3人にその話しを広め、不満に感じた人は33人にその話しを広める」と言ったものです。
つまり、悪いウワサは良いウワサの10倍以上広まりやすいと言ったことになります。
1対5の法則
1対5の法則とは「新規の顧客を開拓し商品を販売には既存顧客に販売するよりも5倍のコストがかかる」と言ったものです。
多くの企業が新規の顧客獲得に力を入れています。もちろん、事業拡大には新規の顧客獲得が必要不可欠ですが、新規の顧客獲得には非常に手間や費用がかかることから、1度でも取引があった既存顧客を維持していくことが大切であると言ったのが1対5の法則です。
5対25の法則
5対25の法則とは「5%の顧客離れを抑えることができれば25%の利益改善がなされる」と言ったものです。
上記の1対5の法則と同様に事業の拡大や売上の拡大と言った場合、新規の顧客獲得に目が行きがちですが、既存の顧客離れを減らすことでも利益が増えると言ったことへつながるといった法則です。
90対9対1の法則(1%の法則)
1%の法則とも呼ばれることがある90対9対1の法則とは「ネット上のコミュニティ参加者よりもROM(リードオンリーメンバー)の方がはるかに多い」と言った法則のことです。
例えばネット掲示板を「見るだけの人」、「たまに書き込む人」、「頻繁に書き込む人」、と言った人の割合が90対9対1になると言ったものです。
実際に、ファミ通.comによるスマホゲームユーザー全体の課金に関する調査では、1年間でスマホゲームに課金したユーザーの割合は9%と言った調査結果が出たと言っています。つまり、残りの91%は非課金者と言うことになります。
また、課金者の内で5001円以上の課金を行った方は7%(全体の0.63%)となっていることから、完全に一致とは言えないもののおおよそ90対9対1の法則が成り立っています。
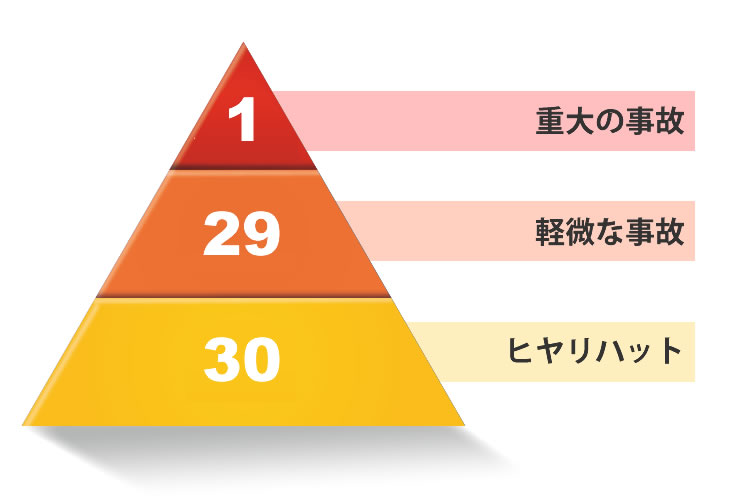
ハインリッヒの法則
ハインリッヒの法則とは1件の重大の事故の裏側では29件の軽微な事故が発生しており、さらに300件のヒヤリハット(ヒヤッとした・ハッとした)が存在していると言った法則のことです。
個人情報の流失や異物混入、交通事故と言ったビジネスシーンで起こりうる重大事故は29件の軽微な事故や300件のヒヤリハットを防ぐことで未然に防ぐことができると言われています。
例えば、「デスクの上に資料が出し放し」「メールの宛先間違い」など小さなヒヤリハットを防ぐことで個人情報の流失などを防ぐことができます。
10,000時間の法則(1万時間の法則)
マルコム・グラッドウェル氏の著書の中で紹介された10,000時間の法則とは簡単に言えば、「何を習得したり、その道のプロフェッショナルなるには10,000時間の時間がかかる」といった法則のことです。
つまり1日9時間、毎日欠かさず行えば3年で約10,000時間となることから、何かを3年間、毎日欠かさず行えばその道のプロフェッショナルになれると言ったものです。
ただし、10,000時間練習すれば誰でもスポーツ選手になれるわけではありませんし、3年先に入社した先輩が全員優秀かと言えば必ずしもそうであるとは限らないためこの法則には否定的な意見も多くあります。
72の法則
72の法則とは「金利に72をかけることで投資したお金や借りた借金がおおよそ倍になる年数を計算することができる法則」のことです。
例えば年利1%で投資を行った場合、元金が倍になるのは「72÷1=約72年」となります。また、利息制限法の上限金利である年20%で借金した場合には「72÷20=約3年半」で借金が倍に膨れ上がります。
40-40-20の法則
40-40-20の法則とは「正しいターゲット選定」が40%、「商品やサービス自体の質」が40%、そして「パッケージのデザイン」が20%と言った割合でダイレクトマーケティングが成功するかどうかが決まると言ったものです。
そのためどんなに素晴らしい商品でも適切なターゲティングやパッケージデザインがなされていなければ、成功する確率は非常に低くなってしまいます。
5-2-2-1の法則
5-2-2-1の法則とは上記で紹介した40-40-20の法則にタイミングを追加したダイレクトマーケティング成功の法則のことで、「正しいターゲット選定(ターゲット)」が50%、「商品やサービス自体の質(オファー)」が20%、「提案する時期や時間(タイミング)」が20%、そして「パッケージのデザイン(クリエイティブ)」が10%の割合で重要であると言った法則のことです。
3Bの法則
3Bの法則とは「美人(Beauty)」「赤ちゃん(Baby)」「動物(Beast)」と3つのB(頭文字)を起用した広告は人の目に留まりやすく、好感を持たれやすいと言ったものです。
雑誌や新聞、テレビと言った従来からある広告はもちろん、ネットのウェブ広告や動画広告などにも3Bの法則が利用されています。
600度の法則
600度の法則とは「2月1日からの最高気温を合計し、600度を超えると桜が開花する」といった法則です。
ちなみに開花宣言は標準木と呼ばれる桜が5~6輪咲いた状態で宣言されます。
400度の法則
400度の法則とは「2月1日からの平均気温を合計し、400度を超えると桜が開花する」といった法則です。
上記で紹介した600度の法則と合わせて予想すると精度がより上がるかもしれません。
90対90の法則
90対90の法則とはシステム開発において「コードの最初の90%が開発時間の10%を占め、残りの10%が90%を占める」と言ったものです。
システム開発が当初の予定よりも大幅に進捗が遅れやすいことに皮肉を込めて表現した法則です。
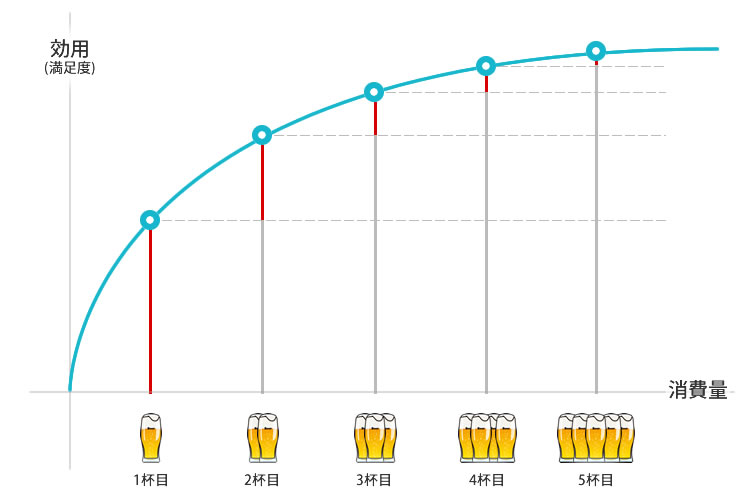
限界効用逓減の法則(げんかいこうようていげんのほうそく)
限界効用逓減の法則とは簡単に言えば、「消費することで得られる満足感は消費する量が増加するほどに低下してしまう」と言った法則のことで、ゴッセンの第一法則と呼ばれています。
例えば、仕事終わりの1杯も2杯目になると1杯目ほどの満足度は得られず、3杯目、4杯目と回数が増えるごとに満足度はさらに低下していくと言ったことが限界効用逓減の法則で、最初の得た満足はどんなに消費しても同じようには得られなくなると言ったことです。
限界とはこれ以上ない状態のこと。また、効用とは得られる満足感のこと。そして、逓減(ていげん)とは徐々に減っていくと意味になります。
限界効用均等の法則(げんかいこうようきんとうのほうそく)
ゴッセンの第二法則と呼ばれている限界効用均等の法則とは、例えば、あなたが大のビール好きであり、上で紹介したように1杯、2杯、3杯・・・と立て続けにビールだけを飲んだとします。しかし限界効用逓減の法則によって徐々にビールによる満足感は低下していきますので、焼酎を飲んだ方が満足できるとなれば、焼酎に切り替えるはずです。そして焼酎を飲み続けていくうちにビールと同様に徐々に満足度は低下していきますので、ワインやウイスキーと言った物に切り替えていきます。
つまり、ビールであれ、焼酎であれ、ワインであれ、限界効用逓減の法則によって満足度が低下するたびに「追加で」消費した際に得られる満足が高い方を人は無意識に選択していると言うのが限界効用均等の法則で、追加することで得られる満足度は、全ての消費において等しくなるといったものが限界効用均等の法則です。
マシュマロの法則
マシュマロの法則とは簡単に言えば「自制心の強い人は成功しやすい」と言った法則です。
マシュマロをあげる際に「少し食べずに我慢したらもう1個マシュマロをあげるよ」と言った実験を子供に行った所、マシュマロを食べてしまった子供よりも食べずに我慢した子供の方が社会的地位の高い仕事などについたと言った実験結果からきた法則です。
マーフィーの法則
マーフィーの法則とは「失敗する余地があるなら、失敗する」と言ったものです。
代表的な例では「落としたトーストがバターを塗った面を下にして着地する確率は、カーペットの値段に比例する」と言った物がありますが、法則の真偽よりもその面白さから話題となった法則です。
仕事で例えるならば、「受注できないと思った案件は受注できない」「仕事の後に予定を入れた日には残業になる」「遅刻してはいけない日に限って電車が遅延する」と言ったことが起きてしまうのもマーフィーの法則によるものだと言われています。
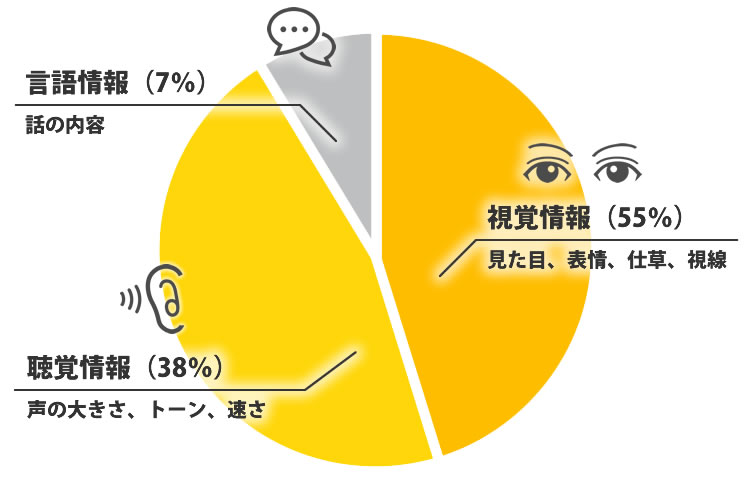
メラビアンの法則
メラビアンの法則とは「表情や目線などの視覚情報が55%、声の大きさや口調と言った聴覚情報が38%、言葉の意味である言語情報は7%と言った割合で人はコミュニケーションにおいて矛盾が生じた場合に重要度を決めている」といった法則のことです。
つまり、話の中で矛盾を感じると相手は話している内容よりも視覚や聴覚による情報を重要視する傾向にあり、あなたの見た目(視覚)はもちろん、話し方(聴覚)などから話の重要度を判断しています。
パーキンソンの法則(第1法則)
パーキンソンの法則の内の第1法則とは、「仕事の量は、完成のために与えられた時間をすべて満たすまで膨張する」と言ったもので、大英帝国(イギリス帝国)が縮小したにも関わらず職員の数は年々増加したことなどから導き出された法則です。
例えば、「本来であれば30分で終わるはずの会議も1時間と言う時間を与えられると1時間をフルに使い会議が行われる」と言ったものです。
パーキンソンの法則(第2法則)
パーキンソンの法則の内の第2法則とは「支出の額は、収入の額に達するまで膨張する」といった法則のことです。
例えば、月収20万(収入)の方は毎月20万円の支出を行ってしまい、仮に月収30万円に増えたとしても増えた分の10万円を貯金にまわすのではなく毎月30万円の支出を行ってしまうと言ったのがパーキンソンの法則の第2法則です。
ムーアの法則
インテルの創業者であるムーア氏によって提唱されたムーアの法則とは「半導体集積回路に使用されている電気の流れを制御する部品であるトランジスタの数が18ヶ月ごとに2倍になる」と言った法則のことです。
現在は「24ヶ月ごとに2倍」に修正されましたが、急速に増加することから近い将来に物理的な限界値を超えるとされています。
グレシャムの法則
イギリスの大富豪であるグレシャムによって提唱されたグレシャムの法則とは、「悪貨は良貨を駆逐する」と言った法則のことです。
簡単に言えば、金の含有量が少ない金貨(悪貨)と金の含有量が多い金貨(良貨)を同時に市場に出した場合、人々は良貨を手元に置いておきたいために悪貨を使用する。そのため市場では悪貨が頻繁に使用されることになり、次第に良貨の方が排除されてしまうと言ったものです。
計画のグレシャムの法則
計画のグレシャムの法則とはノーベル経済学賞を受賞したサイモン氏よって提唱された「ルーチンワークはノン・ルーチンワークを駆逐する」と言った法則のことです。
簡単に言えば、日々のルーチンワークによって創造性(ノンルーチンワーク)が駆逐されると言ったことで、経営者で言えば長期的な計画や新しい事業の創造言ったことが後回しされてしまい、従業員で言えばルーチン化した日々の業務に追われてしまうことで業務の改善案を考えなくなってしまったり、思いついても実行しなくなってしまうというのが計画のグレシャムの法則です。
ピーターの法則
ピーターの法則とは簡単に言えば、能力主義の階層社会おいて社員は能力分だけ出世すると言った法則のことで、能力のない社員は平社員のままですが、能力のある人は出世を繰り返し、能力の限界まで出世するため限界まで出世するとその役職(ポジション)において無能な管理職となってしまう。
そのため、その組織はまだ出世しきっていない社員によって業務が遂行されており、最終的には全てのポジションが無能な社員で埋め尽くされてしまうと言った法則です。
有名選手がコーチや監督になると結果が出せないのもピーターの法則によるものかもしれないと言う方もいます。
グロッシュの法則
グロッシュの法則とは「コンピューターの性能は、価格の2乗に比例する」と言った法則です。
グロッシュの法則通りであれば3万円のパソコンと10万円のパソコンにおける性能比は9対100となります。そのため、予算が許すのであれば高いコンピューターを導入した方がコストパフォマンスは良くなることになります。
しかし実際にはコンピューター価格の相場が下がったことに成り立たなくなったとも言われています。
ブルックスの法則
ブルックスの法則とは「遅れているソフトウェアプロジェクトへの追加要員は、プロジェクトをさらに遅らせるだけである」いった法則です。
ブルックスの法則は主に3つ理由から成り立っています。
1つは追加されたメンバーにプロジェクトの概要を説明したり、現状の報告などしなければならずにすぐに力になるとは限らないこと。2つ目の理由はメンバーが追加されることでプロジェクトメンバーの人数が増えコミュニケーションコストが増えること。そして最後の3つ目はメンバーごとに振り分けられるタスクには限界があることです。
ディルバートの法則
ディルバートの法則とは「企業は、事業への損害を最小限に食いとめるために、無能な人を管理職へ昇進させる」と言った法則で、アメリカの漫画家であるスコット・アダムス氏が提唱しました。
ほとんどの企業で生産性のある仕事に従事しているのは下層に位置する社員であり、管理職に昇進すると生産性のある仕事から外れることになります。
そのため、企業は生産現場から無能な社員ほど昇進させてしまうといったのがこの法則です。
企業はもちろん様々な組織に対して成立する可能性があり、管理職についている上司の中に、もしも無能な社員がいれば、その会社ではディルバートの法則が成り立ってしまいっているかもしれません。
ヒックの法則
ヒックの法則とは選択肢が多くなるほど決断に時間がかかってしまうと言った法則です。
つまり、反対に言えば選択肢を少なくすれば決断にかかる時間は早くなるといったことになります。
たとえば、企業にサービスなどを提案する場合、数多くのプランを用意しお客にその中から最適だと思う物を選ばせるよりもこちから最適なプランを絞って提案する方が早く決まりやすいと言ったことになります。
対外的なものだけでなく、上司などに何かを提案する場合などに同様のことが起こり得やすくなります。
ヴィルトの法則
ヴィルトの法則とは「ソフトウェアは、ハードウェアが高速化するより急速に低速化する」と言ったものです。
簡単に言えばパソコンなどのハードウェアが年々高速化していっていますが、WordやExcelなどのソフトウェアが年々複雑化することで処理に時間がかかることやセキュリティなどの対策のためにシステムが肥大化しソフトウェアは低速化していることからヴィルトの法則が成り立つと言われています。
ホフスタッターの法則
ホフスタッターの法則とは「作業にはいつでも予測以上の時間がかかるものである(ホフスタッターの法則を計算に入れても)」と言った法則で、ダグラス・リチャード・ホフスタッター氏が提唱した法則です。
業務を行う場合ある程度かかる時間の予測を立ててから行動すると思いますが、実際には予測していたよりも作業量が多かったり、別の仕事が舞い込んだりと予想していた時間よりも多くの時間がかかると言った法則です。
また、仕事だけでなく何に対してもホフスタッターの法則はあてはまり、仮にホフスタッターの法則に則って余裕を持たせたとしてもそれ以上の時間がかかると言ったことになりやすいと言ったのがホフスタッターの法則です。
エメットの法則
エメットの法則とは「仕事を先延ばしにすることは、片付けることよりも倍の時間とエネルギーを要する」と言ったものです。
先延ばしにしたことで失敗した経験は社会人であれば誰もが1度は経験したことがあると思いますが、先延ばしにしたことから作業内容を忘れてしまい思い出すのに時間がかかってしまったり、先延ばしにしたことで問題がさらに大きくなり解決に時間がかかってしまったと言ったのがエメットの法則の法則です。
スタージョンの法則
スタージョンの法則には2つの法則があり、1つ目は「どんなものも、その90%はカス(crud)である」と言ったものです。そしてもう一つは「常に絶対的にそうであるものは、存在しない」と言った法則です。
ディヘイの法則
ディヘイの法則とは「簡単な仕事は、いつでもできると言う理由で、常に先送りされる」と言ったものです。
毎月月末に追い込まれてしまっている方はもしかしたらディヘイの法則によって必然的に生じてしまっていることなのかもしれません。
ポッターの法則
ポッターの法則とは「ある問題に対して寄せられる非難の数は、その問題の真価に反比例する」と言ったものです。
今までなかった新しいものが登場した際には否定されることが多いですが、本当に価値があるものほど否定の声は多くなると言った法則です。
メイヤーの法則
メイヤーの法則とは「事態を複雑にするのは単純な仕事だが、単純にするのは複雑な作業である」と言ったものです。
簡単な仕事を依頼したのに複雑化させてしまう癖がある人はメイヤーの法則が働いているのかもしれません。
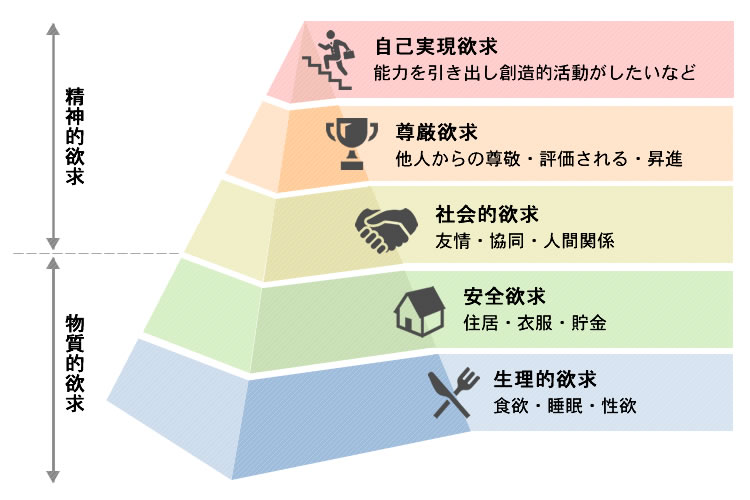
マズローの法則(欲求5段階説・欲求段階説)
マズローの法則とは心理学者であるマズローが「人間は自己実現に向かって絶えず成長する」と提唱し、人の欲求は「生理的欲求」「安全欲求」「社会的欲求」「尊厳欲求」「自己実現欲求」と言った5階層に分かれていると言った法則で、欲求5段階説や欲求段階説とも呼ばれています。
簡単に言えば人は最初の「生理的欲求」が満たされると次の「安全欲求」を欲し、「安全欲求」が満たされると上の「社会的欲求」「尊厳欲求」「自己実現欲求」と段階的に欲するといった法則です。
そのため一度満たされてしまった欲求は次の動機や活力とはなりません。
ランチェスターの法則
ランチェスターの法則とはもともと戦争で使用されていた法則で槍や剣といった原始的な戦闘における第1法則と銃やマシンガンと言った近代的な戦闘における第2法則がありますが、現在ではビジネスの場でも利用されています。
簡単に言えば第1法則は1対1の戦いでは、武器の優劣で勝敗が決まりますが、第2法則は1対多の戦いでは武器の優劣ではなく兵力で勝敗が決まります。
つまり、素晴らしい商品や技術(武器)を持っていても社員数(兵数)が少ない中小企業や零細企業は大企業が存在する市場においてどんなに社員を投入しても勝つことはできませんが、大企業が存在しないニッチな市場であれば社員が少なくとも商品や技術(武器)の優位性で勝つことができます。(弱者の戦略)
反対に大企業は、大量の従業員や資金などを投入することで、他社を圧倒しシェアを獲得することができます。(強者の戦略)
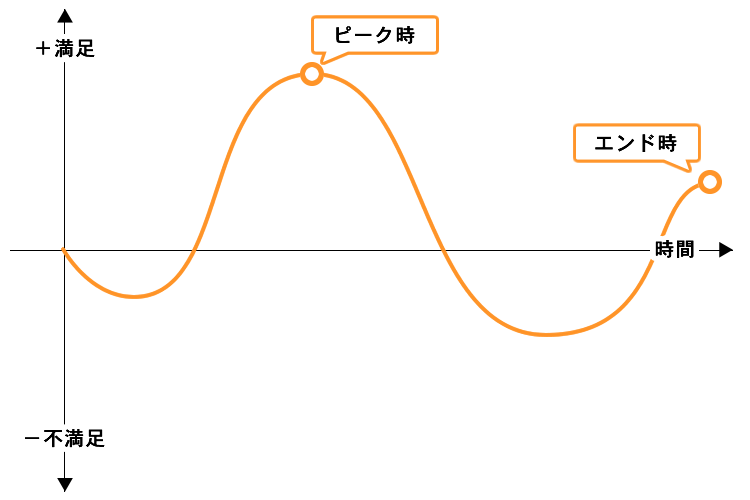
ピーク・エンドの法則
ピーク・エンドの法則とは簡単に言えば、人はピーク(絶頂やどん底)とエンド(最後)で物事を判断しており、ピーク時やエンド時以外の情報は失われることはないが、判断材料としていないと言った法則です。
- A:60秒間、苦痛を感じるほど冷たい水に手を付ける
- B:Aと同じ温度の水に90秒間手をつけるが、60秒を超えると水の徐々に温度が上昇する
この両方の実験を受けてもらった後に、再度AかBの実験を選ばせると、冷たい水に付けている時間が短いAの方が苦痛は小さいはずにもかからず、最後には苦痛が和らいだBの実験をほとんどの被験者が選ばれたと言った結果から導きだされた法則です。
そのため、アウトレットに買い物に言った場合、ピークにあたる「安い買い物ができたこと」や「家族と楽しい食事ができた」などのピーク時の記憶と「渋滞にはまった」などのエンド時の記憶でその日がどうだったのか判断していることになります。つまり、試着室に並んだことやレストランの値段が高かったことなどは忘れはしないものの判断の材料とはしないと言ったことがピーク・エンドの法則です。
一貫性の法則
人間は発言や行動などに一貫性を持たせたがると言うのが一貫性の法則です。つまり、前にした発言(行動なども)に対して矛盾が生じないように発言(行動)をすると言ったものです。
例えば「遅刻は許せない」という方は自分が遅刻しないように行動することや一度ファンになったチームを途中で変えたりしないこと、朝起きて出社するまでの行動(歯磨き、着替えなど)も毎日同じ順番で行おうと無意識にすることは一貫性を法則によるものです。
一貫性の法則はビジネスシーンでも様々な応用方法がありますが、例えば
- 「小さいテレビよりも大きいテレビの方がいいですよね」
- 「画質はキレイな方がいいですよね」
- 「音もキレイな方がいいですよね」
- 「知らないブランドよりも有名ブランドのテレビの方がいいですよね」
- 「高画質・高音質で○○メーカーの最新型50インチテレビが発売されましたがいかがですか?」
と言ったように「YES」と言いやすい質問を繰り返すことで人は一貫性を持たせたいと無意識に意識が働くため営業トークとしても活用されています。
引き寄せの法則
引き寄せの法則とはいわば「願えば叶う」と言った法則で、「こうしたい・こうなりたい」と言ったことを願えばそのようになると言ったものです。
真偽のほどは定かではありませんが、「昇進したい」と思っていればいつかは昇進でき、「副業で稼ぎたい」と願えば稼げるようになると言った法則です。
また、「会社に遅刻しそう」「上司に怒られそう」と言ったネガティブな物を含まれ、「遅刻しそう、遅刻しそう」「怒られそう、怒られそう」と思えば思うほど引き寄せてしまいそのとおりになってしまう可能性が高くなります。
カルマの法則
カルマの法則とは日本語で言えば因果応報のことで、「よい行いをすればめぐりにめぐって自分によい結果が返ってき、悪い行いをすれば悪い結果が返ってくる」と言ったものです。
よく経済なども「消費者がお金を使う」→「企業が潤う」→「社員に還元する」→「給与が増える」と言ったような循環もこの法則によって成り立っていると言われています。
ボッサードの法則
ボッサードの法則とは男女間では物理的な距離と心の距離は比例すると言ったことで、物理的な距離が近ければ近いほど上手くいきやすく、遠ければ遠いほど失敗しやすい、破綻しやすいと言った法則です。
例えば、「合コンで近くに座った人ほど上手くいきやすい、遠くに座った人とは上手くいかないといったこと」や「遠距離恋愛になった途端上手くいかなくなる」と言ったことです。
ジャムの法則
ジャムの法則とは選択肢が多いと人は悩んで買わなくなると言ったものです。
売り場に6種類のジャムを並べた場合と24種類のジャムを並べた場合、24種類の方が多くの人を集めたが3%の人しか買買わず、6種類のジャムを並べた方は30%の人が購入したと言った実験結果からきた法則です。
ただし、売上がどうなったかは含まれていません。24種類の方は3%の人しか買ってくれなかったとしても6種類より圧倒的に多くの人を集められたとすれば売上は24種類のジャムを並べた方が多くなることもあります。
チズホルムの第一法則
チズホルムの第一法則とは「うまくいっている時は、なにかがおかしくなっている」と言った法則です。
「会社に禁止されている副業が毎年順調に伸びている」「バレずに社内恋愛が続いている」と言ったように何かが上手く言っているときほど気をつけないと足元を救われやすいと言ったものです。
チズホルムの第一法則の発展型
チズホルムの第一法則の発展型とは「これ以上悪くなりようのない物事も、悪化する」「順調に見える時は、何かを見落としている」と言った法則です
ドレイゼンの復元力の法則
ドレイゼンの復元力の法則「おかしくなった状況を復元するための時間は、おかしくなるのに要した時間に反比例する」と言った法則です。
「5キロ太るよりも5キロ痩せる時の方が時間がかかる」や「信頼関係を作るのにかかった時間よりも、一度失った信用を取り戻す時の方が時間がかかる」と言ったような法則です。
KISSの法則
KISSの法則とは「簡潔・単純にしておけ!バカ!」と言った意味の「Keep it simple, stupid.」の頭文字からきており「何事もシンプルにしておけ」と言った法則です。
複雑に作ったシステムやアプリは、のちに修正する人から見ると分かりにくく、どのような書き方がされているのか理解するだけで時間も労力も要します。一方、KISSの法則に従ってシンプルに作られていれば何を修正すればいいのか?どこに何が書かれているのかがすぐに理解できます。
他にも資料や作業工程など様々な業務にKISSの法則は応用することができ、何事もシンプルに考え作ることが大切です。
開放性の法則
開放性の法則とは「プライベートな面を知ると相手は親近感を持つ」と言った法則です。
仕事では非常に厳しい人でも「家族に甘い」「動物好き」と言ったようなプライベートな面を知った時から親近感を持ちやすいと言ったものです。
返報性の法則
返報性の法則とは「相手になにかしてもらうと、人は何かを返そうとする」と言ったものです。
お土産をもらうとお返しにお土産を買っていこうと思うのは返報性の法則よるものだと言われています。
また、ビジネスの場でも利用されており、スーパーの試食や化粧品売場で渡される試供品などは返報性の法則を利用した販売戦略の1つです。
さらに「対抗心を燃やせば相手も対抗心を燃やす」と言ったことや「席を譲れば相手も席を譲る」と言ったことも返報性の法則によるものです。
類似性の法則
類似性の法則とは「自分と似ている相手には好意を持ちやすい」と言った法則です。
同じ出身地や同じチームのファン、同じ趣味と言った人には好意を持ちやすいのもこの法則によるものだと言われています。
希少性の法則(希少性の原理)
希少性の法則とは「人は希少性の高いものは価値が高いと思ってしまう」と言ったものです。
例えば「期間限定」「数量限定」と書かれた商品は「今しか買えない」「二度と手に入らない」と言った心理が働き、勝手にその物やサービスの価値を高めてしまうと言った法則です。
ガウゼの法則(競合排除の原理)
ガウゼの法則とは「2種の生物は,同時に同じ生態的地位を占めることはできない」と言った法則です。
実際に2種類のゾウリムシを一緒に飼育すると片方だけが増殖し、もう片方は駆逐されていったそうです。
仮にエイリアンが地球にやってきて、住むことになってもガウゼの法則が正しければどちらが滅んでしまうことになります。
アロンソンの不貞の法則
アロンソンの不貞の法則とは「付き合いの短い人に認められる(褒められる)方が付き合いの長い人に認められるよりも満たされやすい」と言ったものです。
例えば家族や彼女、または会社の同僚などに「○○さんは頑張っているね」と言われるよりもお客に「○○さんは頑張っているね」に言われた方が満たされやすいと言った法則です。
カニンガムの法則
カニンガムの法則とは「インターネット上で正しい答えを得る最良の方法は質問することではなく、間違った答えを投稿することである」と言ったものです。
ネット上で困っている人がいてもわざわざその答えを教える人は少ないですが、間違った投稿に対して指摘せずにはいられないと言った人がいます。
そのため「○○アプリの使い方が分かりません。教えてください。」と投稿するよりも「○○アプリは☓☓すれば△△できる」と間違った投稿した方が正しい答えを得ることができると言った法則です。
ベターリッジの見出しの法則
ベターリッジの見出しの法則とは「疑問符で終わる見出しはすべてNOという言葉で答えることができる」と言ったものです。
新聞や雑誌、ネットニュースなどに「夢は願えば可能のか?」や「虫歯は遺伝するか?」と言った見出しの記事があった場合、答えがNOになるから見出しに疑問符がつけられていると言うのがベターリッジの見出しの法則です。
スキットの法則
スキットの法則とは「他人の誤りを指摘する投稿には、少なくとも1つの誤りが存在する」と言ったものです。
例えばネット上投稿に「そこは大宮市じゃなくて埼玉市だろ」と言った指摘には「埼玉市」ではなく「さいたま市」と言った間違いが存在していると言ったような法則です。
シャーキーの法則
シャーキーの法則とは「組織は自分自身がその解決策となるべき問題を維持しようとする」と言ったものです。
例えば、経費を削減するためにコピーの際は裏紙を極力使用するようにしたものの、汚れた裏紙やよれた裏紙をしたことでコピー機の修理代が高くついたと言ったことです。
ズーニンの法則
ズーニンの法則とは「最初の4分間が大切」と言った法則です。
例えば「仕事などでも最初の4分が上手く行けばその後も上手く進みやすい」と言ったことや「はじめて会った人の印象は最初の4分間で決まる」と言ったものです。
そしてこの4分間は「初動の4分間」と呼ばれています。
ジャネーの法則
ジャネーの法則とは簡単に言えば「生涯のある時期における時間の心理的長さは年齢の逆数に比例する」と言ったものです。
1日や1年と言った時間は何歳になってもその長さ自体が変わるものではありませんが、歳と共に1日、1年が早く感じた経験をしたことがあると思います。この法則は心理的に感じる時間長さは年齢によって異なり、5歳の1年は50歳の10年に相当すると言った法則です。
そのため、ジャネーの法則によれば20歳を超えると人生の半分以上が終わっていることになります。
RICEの法則
RICEの法則とは「身体が傷害を負った際に早急に執るべき応急処置」に関する法則のことです。
負傷した部分は動かさず安静(Rest)にしておく、負傷した部分を冷却(Icing)し炎症などを抑える、出血がある場合には幹部などを圧迫(Compression)して止血する、同じく出血がある場合は負傷した部分を心臓よりも高い位置に持ち上げ(Elevation)出血の量を減らすと言ったものです。
サーノフの法則
サーノフの法則とは「テレビや新聞などのメディアの価値は視聴者(購読者)の数によってその価値が決まる」と言ったものです。
当然のことですが、この後紹介するSNSなどでは違った法則が成り立ちます。
メトカーフの法則
メトカーフの法則とは「ネットワークの価値は利用者数の二乗に比例する」と言ったものです。
上記でも触れたようにFacebookやTwitter、Instagramと言ったSNSではこのメトカーフの法則が成り立つと言われるため、仮にあるテレビ番組の視聴数が10万人で、あなたのTwitterのフォロワー数が同じ10万であればその人Twitterアカウントにはそのテレ番組の10万倍の価値があると言ったことになります
ヤーキース・ドットソンの法則
ヤーキース・ドットソンの法則とは「学習活動に対する動機づけは適切なレベルにあることが必要である」と言ったものです。
ビジネスシーンでも同じことが言え、「売上目標を先月より10%上げる」といった適切なレベルで動機づけを行えば社員は最大限のパフォーマンスを発揮できますが、「売上目標を先月の10倍にする」と言ったように極端に高い目標を与えることや「売上目標を一切廃止する」と言ったように極端に低い目標を与えることは社員のパフォーマンス低下につながる言った法則です。
AIDA(アイーダ)の法則
AIDAの法則とは「消費者が商品やサービスを知ってから購入するまでのプロセス」に関する法則で、Attention(注意)、Interest(興味)、Desire(欲求)、Action(行動)の4つのプロセスを経て購入に至ると言われています。
例えば、広告を通じて消費者の注意(Attention)を引くと同時に興味(Interest)を持たせ、購入したい・欲しいと言う欲求(Desire)を持ってもらうことで購入・来店と言った行動(Action)をもたせることができます。
現在ではホームページやパンフレット、広告などでAIDAの法則は応用されており、ビジネスでは比較的有名な法則の1つとなっています。
AIDMA(アイドマ)の法則
AIDMAの法則とは上記のAIDAの法則に「Memory(記憶)」を追加したモノです。
例えば通勤の中の電車の中で新商品の販売を知っても、その場で購入できるとは限りません。商品やサービスによっては店舗などに来店してもらって初めて購入することができます。そのため、購入意欲を記憶(Memory)しておいてもらうことが重要となります。
AIDAの法則はセント・エルモ・ルイス氏が提唱したのに対して、AIDMAの法則はサミュエル・ローランド・ホール氏が提唱した法則です。
AISAS(エーサス、アイサス)の法則
AISASの法則とはAIDAの法則やAIDMAの法則と同じ「消費者の行動プロセス」に関するもので、AISASの法則ではAttention(注意)、Interest(興味)、Search(検索)、Action(購買)、Share(共有)と言った5つプロセスを経て購入に至ると言われています。広告代理店の電通が提唱した法則です。
特に最近は誰もネットを使うようになっていることから消費者が興味を持ってすぐには購入に至りません。そのためまずはその商品やサービスについて検索(Search)を行ってから購入や来店と言った行動(Action)を起こします。そして行動から得た情報を友人への口コミやネット上へのレビュー投稿などを通じて共有(Share)します。
AIDCA(アイドカ)の法則
AIDCAの法則とは、上記で紹介した行動プロセスに関する法則と言った意味ですがAttention(注目)、Interest(関心)、Desire(欲求)、Conviction(確信)、Action(行動)と言った5つプロセスによって購入や来店と言った行動(Action)に至ります。
決定回避の法則
決定回避の法則とは「人は選択肢が多すぎると選ぶことができなくなる」と言ったものです。
内容は上記で紹介したジャムの法則と同じですが、エルダーシャフィールが提唱した法則です。
現状維持の法則
現状維持の法則とは上記の決定回避の法則を提唱したエルダーシャフィールが提唱した法則で、「人は選択肢の数が増えると、普段と同じような商品を選んでしまう」といったものです。
メニュー数の多いファミレスや居酒屋に無意識の内にいつもと同じメニュー、または同じようなメニューを選んでしまうと言った場合は現状維持の法則のせいかもしれませんし、転職をしたいと思っているが、転職したいと思う企業が見つからないという人も、もしかしたら現状維持の法則が働いてしまっているのかもしれません。
損失回避の法則
損失回避の法則とは「人は利益を得るよりも損失を避けることを選ぼうとする」と言ったものです。
「2人のうち1人に200万円がもらえる」と言ったものより「全員が100万円をもらえる」と言った場合、後者を多くの人が選ぶと言った法則です。
「今月末でポイントが失効します」「今注文すれば、○○をプレゼント」と言ったものも損失回避の法則を応用した戦略の1つです。
マーチンゲール法則
マーチンゲール法則とは簡単に言えば「倍掛けしていけば必ず勝てる」と言ったものです。
例えば100円をかけて負けた場合、次は200円をかけ、400円をかけと言ったように負け続ける限り倍がけしていけば最後は必ず勝てると言った法則です。
FXといった投資の世界やギャンブルの世界では有名な法則の1つですが、上記の例のように100円から倍掛けした場合10回目には5万1200円、20回目に5242万8800円と言った掛金が必要になります。
セイの法則
セイの法則とは「非貨幣市場の総供給と総需要が常に一致する」と言ったもので、簡単に言えば「需要が供給をきめるのではなく、供給が需要を決める」と言った法則です。
例えば、アイスが大量に市場に出回れば売れ残りが出てしまいますが、売れ残り価格が下がることで需要が増え、最終的には売れ残っていたアイスも売り切れます。また、反対にアイスの数が足りなくなれば、しだいに価格が上がり需要が減ると言ったことから考えられたのがセイの法則です。
ジャーディン・フレミングの法則
ジャーディン・フレミングの法則とは「社長が自分の苦労話ばかりする会社は、成長しない」と言ったようもので、現在のJPモルガン・アセット・マネジメントの幹部が日本企業を訪問した際に提唱した法則です。
他にも「体操を社員に強要する会社は儲からない」や「社長が著名人との交際をにおわせたり、強調する時は、その会社への投資を避けたほうがいい」、「社長室の豪華さと、その会社の成長率は反比例する(つまり、豪華であればあるほど、成長率は低くなる)」と言った法則があるそうです。
ランスの法則
ランスの法則とは「物事がうまく運んでいるなら、いらぬ手をくわえるな」と言ったものです。
人気のある商品に手を加えたら良くなるどころか、「使いにくくなった」、「不味くなった」、「不具合が多くなった」、「売上が下がった」と言った法則です
長年付き合っている彼氏・彼女にサプライズをしたら成功するどころか失敗したと言ったこともランスの法則によるものかもしれません。
茹でガエルの法則
茹でガエルの法則とは「ゆっくりとした状況変化には手遅れになるまで気が付かない」と言ったもので、茹でガエル現象などとも呼ばれています。
カエルを熱湯に入れると飛び跳ねて逃げ出しますが、常温にカエルを入れ徐々に温度を上げると茹で上がり最後は死んでしまったことから提唱された法則です。
年金制度の崩壊や年々増加する日本の借金、さらには地球環境の悪化などは大きな問題として多くの人に認知されていますが、徐々に変化していくため茹でガエル状態となってしまいやすい。
波長の法則
波長の法則とは、言うなれば「類は友を呼ぶ」と言ったモノで、「同じ波長の人は相性が合う」「同じ波長の人同士が集まりやすい」と言った法則です。
ヤンキーのまわりにヤンキーが集まり、オタクのまわりにはオタクが集まりやすいと言った法則です。
言い出しっぺの法則
言い出しっぺの法則とは「提案した人が実行させられる」と言った法則です。
例えば「じゃんけんで負けた人が買い出しね」と言い出した人が買い出しに行かされると言ったことや「コピー機用紙がなくても誰も補充しません」と会議で提案すると補充担当に任命されてしまうと言ったものです。
レス・イズ・モアの法則
レス・イズ・モアの法則とは「少なくすれば増える」や「シンプルにすれば増える」といったものです。
例えば、使っていない物を捨てれば家の中が片付き掃除の時間が減る(空いた時間が増える)、家電から不要な機能をなくせば売上が上がると言ったようなものです。
松竹梅の法則(コルディロックス効果)
松竹梅の法則とは「人は選択肢が3つ(松・竹・梅)あると真ん中を選ぶ」と言ったもので、コルディロックス効果とも呼ばれています。
価格の差や商品などによって差が生じますがおおよそ「松2」対「竹5」対「梅3」の割合になると言われており、この法則から真ん中の竹は最も利益率が高くなるように価格設定している店も多いとか少ないとか・・・
ゲシュタルトの法則
ゲシュタルトの法則とは「人は見たものを無意識にまとめる(グループ化)する」と言ったものです。
例えば
●●●●●●●▲▲▲▲▲▲▲▲■■■■■■■
と言った図形が並んでいると
「●●●●●●●」
「▲▲▲▲▲▲▲▲」
「■■■■■■■」
と言ったように自動的にグループ化すると言った法則で、ウェブデザインなどにも応用されています。
グッドマンの第1の法則
グッドマンの第1の法則とは簡単に言えば「商品やサービスなどに不満がある顧客のうち、クレームを言い、その対応に満足をした顧客の再購入率はクレームを言わない顧客よりも高い」と言ったものです。
当然と言えば当然の法則ですが、クレーム対応を適切に行い顧客の満足度を上げることができれば、クレーマーはリピート客になりやすいと言った法則です。
グッドマンの第2の法則
グッドマンの第2の法則とは簡単に言えば「クレーム対応に満足しなかった顧客による悪い口コミは満足した顧客の良い口コミの2倍以上も拡散されやすい」と言ったものです。
特に最近はSNSなどの普及により口コミは拡散されやすい状況であり1つのクレーム対応を間違えただけで、他の商品の売上低下や全体の売上低下にもつながりかねません。
グッドマンの第3の法則
グッドマンの第3の法則とは簡単に言えば「消費者に対して教育を行えば、信頼度が高まり好意的な口コミの波及効果が期待されるばかりか、商品購入意図が高まり、かつ市場拡大に貢献する」と言ったものです。
チャルディーニの法則
チャルディーニの法則とは言うなれば「相手への影響力を高め、相手を思い通りに操る」ための法則で、人間の6つの心理に則った法則です。
1.返報性
なにかをしてもらった相手にはなにかを返そうと思う心理で、試供品などをもらうと商品を買いたくなる、買ってあげようと言ったことです。
2.一貫性
一度決めたことや一度はした発言は一貫性を持たせようとしてしまう心理で、ボランティアに参加したことがある人は募金にも応じやすいと言ったことです。
3.社会的証明
他人の評価を基準に、物事を判断しようとする心理で、「人気のある商品」「全米で大ヒット」と言った社会的に認められている物はよい物であると思ってしまうことです。
4.好意
人は好意を持っている相手から頼まれごとは受けてしまうと言った心理で、友人などに頼まれると断れないと言ったことです。
5.権威
自分よりも高い地位の人に従ってしまう心理で、社長や先輩と言った人の命令に対して逆らいづらいと言ったことです。
6.希少性
少ない物には価値があると思ってしまう心理で、「期間限定」「数量限定」と言った物は無意識の内に良い商品であると思ってしまうことです。
ザイアンスの法則(単純接触効果)
ザイアンスの法則とは「人は接する回数が多いほど警戒心が薄れ、高感度が増す」いったもので、単純接触効果とも呼ばれています。
初めて会った時に特に話をしなくとも、二度目に会った時は話しやすくなっていると言ったことがこの法則です。
ビジネスはもちろん、恋愛などにも応用することができます。
ベンフォードの法則
ベンフォードの法則とは「自然界に出てくる多くの(全てのではない)数値の最初の桁の分布が、一様ではなく、ある特定の分布になっている」と言ったもので、その中でも最初の桁が「1」になる確率は30%以上にもなります。
本来であれば1~9のいずれかになるかで優越はありません(最初の桁が0になることはなし)。そのため本来は1~9になる確率は11.1%となるはずですが下記の表のように偏りが発生していると言った法則です。
| 最初の桁 | 発生する確率 |
|---|---|
| 1 | 30.1% |
| 2 | 17.6% |
| 3 | 12.5% |
| 4 | 9.7% |
| 5 | 7.9% |
| 6 | 6.7% |
| 7 | 5.8% |
| 8 | 5.1% |
| 9 | 4.6% |
出典:ウィキペディア
マジカルナンバー7±2の法則
マジカルナンバー7±2の法則とは「人が短期的に覚えられる数字はおおよそ7個を中心に5~9個である」といったものです。
左回りの法則
左回りの法則とは「人は無意識に反時計回り(左回り)を選択する」と言ったものです。
グラウンド野球のベースなど、ほとんどが左回りに作られているのはこの法則によるものだと言われており、スーパーやコンビニと言った店舗も左回りを基準に店舗内をまわりやすいように作られていることが多く見られます。
「地球の自転や公転が左回り」「心臓が左にある」「重たい肝臓が右にある」「感覚を司る右脳が右にあり、左半身とつながっている」などの理由から左回りの法則が成り立っていると言われています。
努力逆転の法則(エミール・クーエの法則)
努力逆転の法則とは「意思と想像力が相反した場合は想像力の方が勝つ」「意思と想像力がぶつかり合う場合、想像力は意思の2乗に正比例する」「意思の力で努力すればするほど想像力は強くなり意思の努力とは反対の結果となる」と言った3つ定義からなる法則のことです。
例えば「禁煙しよう」と意識すればするほど喫煙の想像力の勝ってしまうと言ったことです。
一物一価の法則(無差別の法則)
一物一価の法則「自由な市場経済において同一の市場の同一時点における同一の商品は同一の価格である」と言ったものです。
大数の法則
大数の法則とは「試行回数を多く重ねることで理論上の数値に近づく」と言った法則です。
例えばコインを投げた場合に表の出る確率と裏の出る確率は50%:50%ですが、10回と言ったように少ない回数試した場合、表(または裏)の方が多く出ると言った偏った結果が出てしまうことがあります。
しかし100回、200回、300回と回数を多く試行することで理論上の50%:50%と言った数値に近づくと言った法則です。
小数の法則
小数の法則とは「人は試行回数が少ないことによって生じた偏った統計結果を正しいと思ってしまう」と言ったものです。
例えば上記で紹介したコインの出現回数において60対40と言った結果が出た場合、実際には試行回数が少ないことにより偏った結果が出たにも関わらず「表と裏で絵面が違うから」「製造過程で原材料に偏りができるから」と言ったようにもっともらしい理由をつけて正しいと信じ込んでしまうと言った法則です。
Zの法則
Zの法則とは「人は何かを見る時に左上→右→左下→右下といった流れで視線を動かす」と言ったものでホームページや雑誌、商品棚などを見る際にはZ字に閲覧しやすいと言った法則です。
ホームページで左上にロゴ、右上にお問い合わせボタンなどがあるのはZの法則を基にレイアウトされるためです。
リトルウッドの法則
リトルウッドの法則とは「奇跡は1ヶ月に1度は起こり得る」と言ったもので、イギリスの数学者であるジョン・エデンサー・リトルウッドが提唱した法則です。
この場合の奇跡を「100万回に1度しか発生しない例外的な事象」と定義し、1秒に1回物事が起きると仮定すると、人が1日に8時間(28,800秒)起きていた場合、35日で100万回を超えるため1ヶ月に1度は奇跡が起きてると言った法則です。

この記事が気に入ったら いいね!しよう