有名な建築物にしても、名画などの美術品にしても、私たちが見て美しいと感じるものには、多くの場合ある共通点があります。それは、「一定の比率で表せる形を持っていること」というものです。こうした比率を持つことにより、人間の目には、その対象が「美しさ」や「安定感」「心地よさ」などを持って映ると言われています。この法則は、私たちの身の回りにある多くの商品やロゴマークなどのデザインにも取り入れられています。

このような美感を呼び起こす比率には、「黄金比」や「白銀比」など、いくつかの種類があります。これらはデザインの世界では有名ですが、一般的にはあまり詳しく知られているわけではありません。

そこでここでは、「黄金比」「白銀比」「青銅比」「白金比」「第2黄金比」といったさまざまな比率について、詳しく解説してみたいと思います。

黄金比とは（第1貴金属比とは）

「黄金比」とは、簡単に言うと、「人間にとってもっとも美しく安定して見える比率」のことです。英語では「Golden Ratio」と呼ばれており、別名「第1貴金属比」とも呼ばれます。

「貴金属比」とは、1：（ｎ+√ｎ2+4）/2の数式で表される比率で、ｎには自然数が入り、それに応じて第1貴金属比、第2貴金属比などと変化します。
いずれも人に安心感や美感を覚えさせるバランスを持っていますが、「黄金比」はその中でも、前述のようにもっとも美しく安定して見える比率となっています。

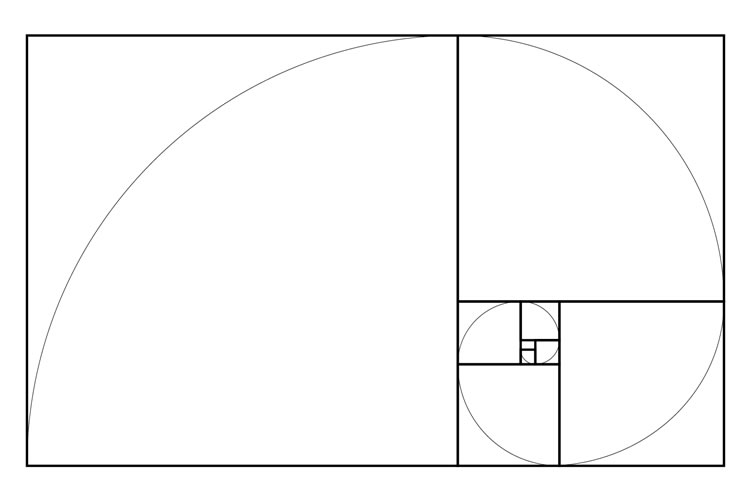
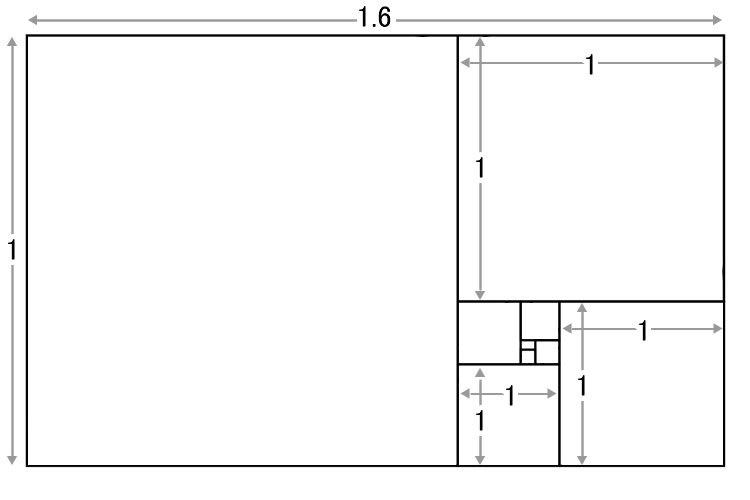
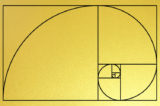
「黄金比」を具体的に数字で表すと、1：（1+√5）/2となります。近似値は1：1.618です。実際には小数点以下は無限に数字が続きますが、およそ1：1.6ほどと覚えておけば問題ありません。この比率で表せるものに対しては、ほとんどの人間が安らぎや美的感覚を呼び起こされるようになっています。

「黄金比」の説明において、頻繁に用いられるのが、「黄金長方形」と呼ばれる長方形です。これは縦横の比率が先ほどの1：1.618となった長方形で、内部に大きさの異なる正方形がいくつも描かれています。正方形を大きなものから除いていくと、また同じ比率を持つ長方形となり、それが繰り返されます。このようなパターンを持ったデザインが、「黄金比」と呼ばれるものです。

それでは、「黄金比」の具体例について、以下でいくつか挙げて説明していきましょう。

ミロのヴィーナス

古代ギリシアで制作された女性像「ミロのヴィーナス」は、「黄金比」を持つデザインの例として、よく挙げられるものの1つです。「ミロのヴィーナス」が美の代名詞として語られるのは、そのプロポーションに黄金比が隠れているためとされています。

例えば「ヴィーナス」の全身をへその部分で上下に分けたとき、上半身が1で、下半身は1.618という比率になります。また下半身を1とした場合は、全身の長さが1.618となります。

モナ・リザ

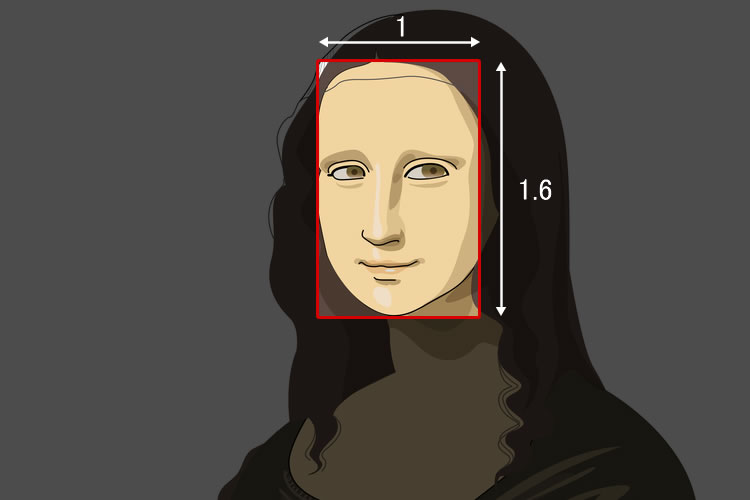
ルネサンス期の巨匠レオナルド・ダ・ヴィンチの絵画「モナ・リザ」もまた、「黄金比」を持つものの代表例としてよく挙げられます。「モナ・リザ」は美術史において最も有名な絵の1つで、古今東西の多くの人を惹きつけていますが、その中にも「黄金比」が見て取れます。

「モナ・リザ」において「黄金比」を表しているのは、視線の集中する顔の部分です。「モナ・リザ」の顔は横が1、縦が1.618と、見事に「黄金比」の比率となっています。

アップルのロゴ

「黄金比」が隠れているのは、何も歴史的な美術品や建造物だけではありません。現代的なデザインにおいても、「黄金比」を持ったものがいくつも見られます。

その例としては、ロブ・ジャノフ氏がデザインした「アップルのロゴ」が挙げられるでしょう。アップルユーザーでなくても、ほとんど毎日見かけるといってもよいくらい有名なロゴですが、その曲線部分を分解していくと、前述の「黄金長方形」の中に収まる円で構成されていることが明らかとなっています。

白銀比とは（第2貴金属比とは）

「白銀比」とは、英語では「Silver Ratio」と呼ばれる比率です。「白銀比」と呼ばれるものには2種類ありますが、その1つが「第2貴金属比」で、この場合は「黄金比」と同じく、貴金属比の一種になります。やはり「黄金比」のように美感や安定感に優れており、さまざまなデザインの中に見られます。
「白銀」の名は、周期表で「黄金」に次ぐ順番の貴金属といった意味合いで付けられています。

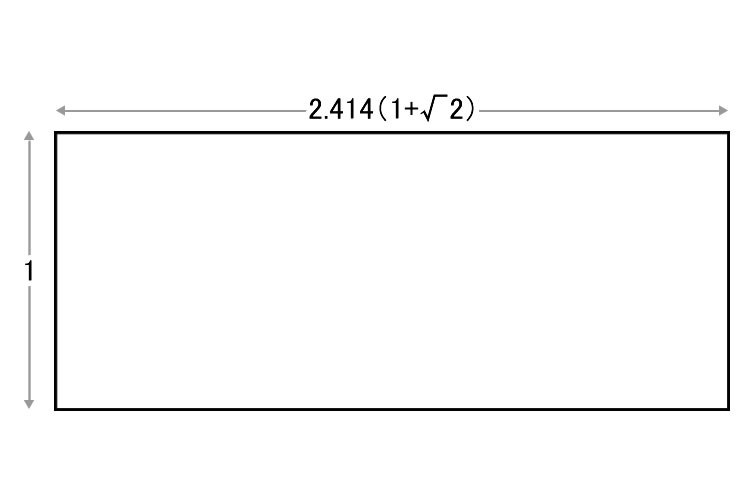
「白銀比（第2貴金属比）」の具体的な数値は、1：1+√2です。別の数字で表せば、1：2.414となります。こちらも「黄金比」同様無理数であり、小数点以下は無限に続きます。整数で表すならば、近似値は5：12となります。

「黄金比」に「黄金長方形」があるように、「白銀比」にも「白銀長方形」と呼ばれるものがあります。これは縦横の比率が1：1+√2となる長方形のことで、後述する「1：√2白銀長方形」とは微妙に異なります。ただ、両者には相関性があり、1：1+√2白銀長方形からもっとも大きい正方形を取り去ると、1+√2白銀長方形となり、反対に1√2白銀長方形からもっとも大きい正方形を取り去ると、1：1+√2白銀長方形となります。

正八角形

では、「白銀比（第2貴金属比）」の例についてご紹介しましょう。こちらの場合の代表例は、正八角形になります。正八角形の中には長方形が形作られますが、その短い辺の長さを1とすると、長辺の長さの比は、1+√2となります。つまり1：1+√2の比率であり、正八角形の中に第2貴金属比が隠れていることになります。

正八角形をかたどったデザインは、時計や鏡などいろいろなものに使われていますが、これらの安定感はこうした比率から来ていると言えます。

白銀比とは（大和比とは）

続いても「白銀比」についての説明ですが、こちらは上記の「第2貴金属比」とは別の、「大和（やまと）比」と呼ばれる種類になります。先ほど述べた通り、「白銀比」には2種類あり、そのうちの1つがこの「大和比」に当たります。

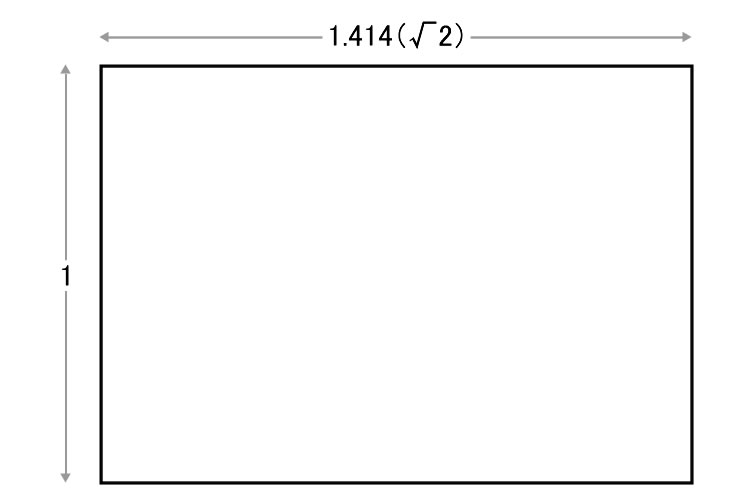
「大和比」を数式で表すと、1：√2（近似値1：1.414）となり、上記の「第2貴金属比」の1：1+√2とは微妙に異ります。しかし、一般的には2つを同じものとして扱うことも多くなっています。

「大和比」という呼び名が付いているとおり、こちらの比率は和風のデザインによく見られるものです。特に仏堂などの日本建築で使われているのが知られており、ほかにも紙の規格で採用されるなど、日本人にとっては「黄金比」以上になじみ深い比率となっています。

前述のように、「白銀比（大和比）」にも「白銀長方形」と呼ばれるものがあります。こちらは前記のものと区別するために「ルート白銀長方形」とも呼ばれますが、縦横の比率が1：√2となっています。この長方形は、長辺で2等分した時に、元のルート白銀長方形と同じ比率の長方形が2つできるのが特徴です。これも前述した通り、この比率の長方形は、ISO 216規格による紙の寸法と一致しています。

法隆寺金堂

「白銀比（大和比）」の例としては、「法隆寺の金堂」もよく名前が挙げられます。法隆寺は聖徳太子ゆかりの寺として、また現存する最古の木造建築物（7世紀創建）としても有名ですが、その西院伽藍最古の建築である「金堂」には、見事な「大和比」の比率が見られます。

「金堂」の2階の幅を1とした場合、1階（礎石部分）の幅は1.4となり、「大和比」の数値にぴったり当てはまります。このような比率もあり、「金堂」は日本人の目にとって安定感のある美しい建物として映るようになっています。

法隆寺五重塔

続いての「白銀比（大和比）」の例もまた、法隆寺にちなむものです。「五重塔」は仏塔の形式の1つですが、法隆寺のものは日本最古の「五重塔」であり、その代名詞ともなっています。金堂や鐘楼などとともに「西院伽藍」の一部をなしており、世界遺産である法隆寺の中でも、金堂と並んで特に有名な建築物です。

その「五重塔」における「白銀比」は、最上層の屋根の幅と、最下層の屋根の幅の比率です。ここにおいても、やはり1：1.4という「大和比」が見て取れます。

ドラえもん

ここまでは、日本の伝統建築などを例として挙げてきましたが、「白銀比（大和比）」は現代日本でもおなじみの比率となっています。そのもっとも有名な例が、アニメや漫画などの「キャラクター」に関するものです。

例えば国民的なキャラクターである「ドラえもん」は、大きな丸い頭と短い胴体や手足が特徴ですが、その横幅と身長を比べると、比率が1：1.414となります。つまり、ここにも「白銀比（大和比）」が見られるわけです。こうした例はドラえもんに限らず、「キティちゃん」の顔などにも見られます。

青銅比とは（第3貴金属比とは）

「黄金比」の説明において、「貴金属比」にはいくつかの種類があると述べましたが、そのうち第3にあたるのが、こちらの「青銅比」と呼ばれる比率です。英語では「bronze ratio」と呼ばれます。

「銅」は周期表では原子番号29に当たる元素ですが、79の「金」、47の「銀」と縦に並んでおり、下から数えて3番目に当たっています。「黄金比」「白銀比」に次ぐ第3貴金属比が「青銅比」であるのは、このような理由があります。

「青銅比（第3貴金属比）」を数式で表すと、1：（3+√13）/2となります。近似値は1：3.303です。青銅比における（3+√13）/2の部分は、二次方程式 x2 -3ｘ-1＝0の正の解であり、これは「青銅数（bronze number）」と呼ばれています。ちなみに他の貴金属比についても、x2 -kｘ-1＝0の正の解として表せます。ｋの値が1であれば「黄金比」となり、2であれば、「白銀比」となります。

「黄金比」や「白銀比」と同様に、「青銅比」もまた、人間にとって美しいと感じられる比率です。ただし、デザインとして使われるケースは、「黄金比」や「白銀比」などに比べ、それほど多くありません。

白金比とは（プラチナ比とは）

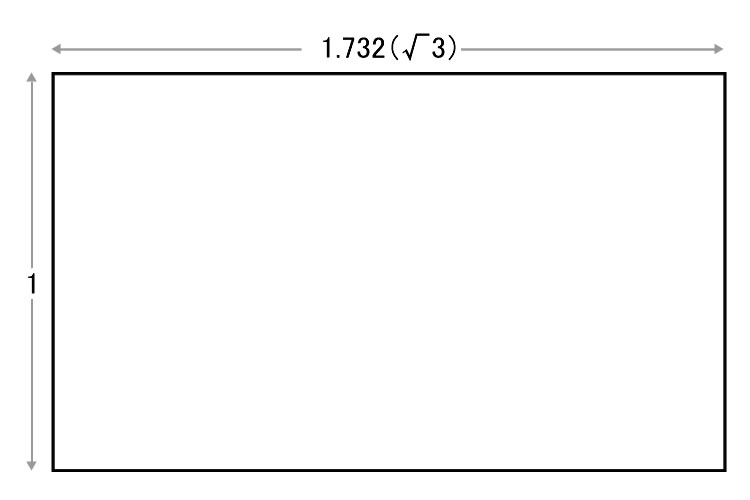
「白金比」とは、英語では「platinum ratio」と呼ばれる比率のことです。「プラチナ比」と呼ばれることもあります。「黄金比」や「白銀比」などともに貴金属の名前が付いていますが、正確には「貴金属比」ではありません。その理由は、比率の数式にあります。「白金比」の数式は1：√3（近似値は1：1.732）となっており、前述した貴金属比の数式1：（ｎ+√ｎ2+4）/2には、あてはまらないことが分かります。

白金比は、正三角形の底辺の1/2の長さと、その三角形の高さの比に等しい定数となっています。

「白金比」は、前述のように貴金属比ではないものの、人間に美感を催させる比率を持つと言われています。そのために、美しい光沢を持ち、ネックレスなどの装飾品としてもよく使われる「白金」の名が冠せられています。

ちなみに白金の原子番号は78で、79の「金」の1つ前に当たります。ただし、「黄金比」や「白銀比」が数多くの身近なデザインに用いられているのに対し、「白金比」を用いたデザインは、「青銅比」同様私たちの周辺にはあまり見当たりません。その理由は定かではありませんが、理論的には美しさを表す比率であるのは確かです。

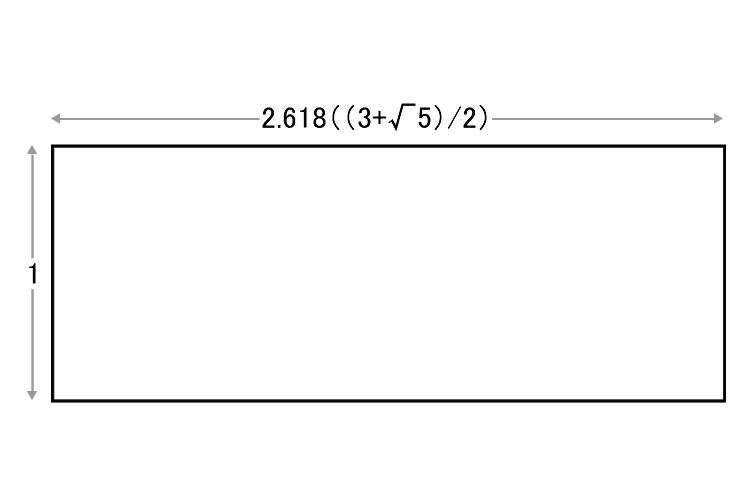
第2黄金比とは

「黄金比」とは別に、「第2黄金比」と呼ばれる比率も存在します。こちらの比率を数式で表すと、1：（3+√5）/2となります。近似値は1：2.618で、整数では約3：8の比率となります。長方形にした時の長辺の長さは、「青銅比」（1：3.303）に次ぐ長さとなっています。
ちなみにその次が「黄金比」（1：1.618）で、「白銀比」（1：1.414）はもっとも短い比率となります。

「第2黄金比」は、「黄金比」と名前が付いているものの、貴金属比の1つではありません。貴金属比は前にも述べたように、1：（ｎ+√ｎ2+4）/2の数式で表されるものです。「第2黄金比」は一見この数式に似ていますが、実際には当てはまることはなく、貴金属比とは別物の比率となっています。にもかかわらず「黄金比」の名前が付いているのは、先にも述べた通り、「黄金比」に次ぐ長さの比を持っているためです。

このように、「第2黄金比」は貴金属比ではありませんが、「黄金比」などと同様に、理論上美しく均整の取れた比率とされています。しかし、これに関しても、「青銅比」や「白金比」のように身近なデザインで使われている例は見当たりません。「黄金比」に比べると、かなりマイナーな比率となっています。