デザイン
黄金比の意味とは?黄金比の実例25選
スポンサーリンク
「黄金比」という言葉については、どこかで触れたことがあるという人がほとんどでしょう。とは言え、ものの形の比率であることや、審美的な基準であることは知っていても、それ以外のことはよく分からないという人も多いのではないでしょうか。実際に、概念自体は古くからあるものの、「黄金比」という言葉が作られたのは意外に新しく、一般の人にとってそれほどなじみ深いものとは呼べないようになっています。
しかし実は、「黄金比」は商品などのデザインや古今東西の美術品や建築物、果ては自然が作り出したものにまで見つけることができる、身近な存在でもあります。
ここではそうした「黄金比」の意味や実態について、さまざまな角度から解説するとともに、具体的な事例についてもいくつか挙げて紹介していきたいと思います。
黄金比とは
黄金比とは?
「黄金比」とは、「貴金属比」と呼ばれるものの1つです。「貴金属比」とは、人間が見て美しさや安定感を感じる比率を意味しており、「黄金比」はそのうち「第1貴金属比」にあたります。英語では、「golden ratio」と呼ばれています。
「黄金比」は、数式で表すことができます。1:(1+√5)/2というのがそれで、別の数字で表すならば、1:1.618となります。実際には小数点以下無限に数字が続きますが、近似値は1:1.61と覚えておけば問題ありません。
「黄金比」は先に述べた通り、人間にとって美しいと感じられる比率の一種であり、その中でも特に美感や安定感に優れているとされています。特に西洋ではその傾向が強く、さまざまな建築や美術、商品のデザインなどに「黄金比」が取り入れられています。
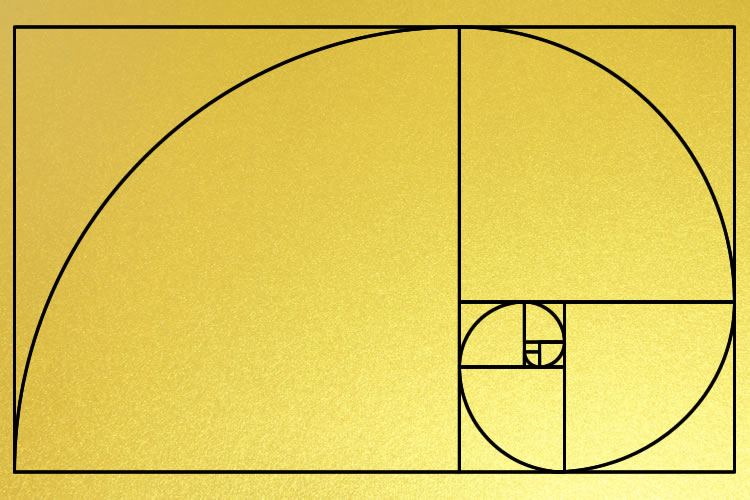
黄金長方形とは?
「黄金長方形」は、「黄金比」の説明においてよく用いられる図形です。その名の通り、縦横の長さが「黄金比」の比率から成る長方形を意味します。すなわち、短辺と長辺の比が1:1.618となるものです。
「黄金長方形」の図形では、さらに内部にいくつもの正方形が描かれます。それらの大きさはそれぞれ異なっており、そこから最大のものを除くと、再び「黄金比」を持った長方形ができるのが特徴です。以下、同じ操作によって無限に同じ図形が得られるようになっています。
「黄金長方形」は、定規とコンパスを使って簡単に書くことができます。まず正方形を描き、一辺の真ん中を中心として、そこから向かい合う辺の頂点までを半径とする円弧を描きます。中心の辺の延長と円弧が交わる点を新たな頂点とし、同じ要領でもう1つの頂点を作れば、「黄金長方形」が出来上がります。
黄金螺旋とは?
「黄金螺旋」とは、「黄金比」に関連した螺旋形です。「対数螺旋」と呼ばれるものの一種になります。「対数螺旋」とは、一定の数式で表される螺旋形を意味し、「等角螺旋」や「ベルヌーイの螺旋」とも呼ばれ、自然界でもよく見られる形状となっています。
「黄金螺旋」は、前述の「黄金長方形」から得ることができます。「黄金長方形」の中に、多数の正方形が描かれることは上でも述べましたが、その正方形の頂点を螺旋状につないでいくと、「黄金螺旋」が現れるようになってます。
先ほど「対数螺旋」が自然界のいろいろな場所で見られると述べましたが、「黄金螺旋」も例外ではありません。一番有名な例は「オウムガイの殻」で、その模様は「黄金螺旋」の形状に近いと言われています。
黄金比の歴史
「黄金比」の概念自体は、前述のように古くから知られていました。発見したのはエウドクソスという古代ギリシアの数学者で、始めて使ったのは、伝承によるとやはり古代ギリシアの彫刻家ペイディアスであるとされています。現在使われている「黄金比」の記号φは、ペイディアスの頭文字を意味します。ペイディアスが「黄金比」を用いて作ったのは、古代ギリシア建築の傑作として知られるパルテノン神殿でした。それとは別に、レオナルド・ダ・ヴィンチもまた「黄金比」を発見していたと言われています。
「黄金比(golden ratio)」の言葉が文献で使われたのは、1835年が最初になります。ドイツの数学者マルティン・オームの著書『初等純粋数学』においてでしたが、以後「人間にとって最も美しい比率」として広まり、先にも述べた通り、さまざまなデザインに利用されています。
黄金比の実例
上の項でも何度か述べたように、「黄金比」を用いたデザインは、古今東西の美術品や建築物などに数多く見られます。
ヨーロッパでの使用が特に多くなっていますが、日本でもいくつかのデザインに、その比率が見て取れます。意識して取り入れたものだけでなく、偶然そうなった例もありますが、いずれにせよ、私たちが見て美しさを感じるものの中に、高確率で「黄金比」が隠されています。
ここではそうしたものの中から、いくつかの例を選んでご紹介していきましょう。
サグラダ・ファミリア
最初にご紹介する「黄金比」の事例は、スペインの「サグラダ・ファミリア」です。バルセロナにある世界的に有名なカトリック教会で、これもまた著名な建築家、アントニオ・ガウディの代表作として知られています。大胆で複雑、かつ優美なフォルムを持つデザインから多くの人々を惹きつけ、バルセロナ市のシンボルとして、世界中から観光客を集めています。「サグラダ・ファミリア」における「黄金比」は、全体の高さと幅の長さの比率に現れています。
パルテノン神殿
「パルテノン神殿」は、古代ギリシアでアテナイのアクロポリスの上建設された、神話の女神アテナを祀るための神殿です。上でも述べたように、建設においては古代ギリシアの彫刻家ペイディアスが監督を務めたとされています。
建設が始まったのが紀元前447年で、その後紀元前438年に完工しましたが、装飾等については紀元前431年まで行われました。
パルテノン神殿は前述のように「黄金比」が使われた最初の建築物とされ、正面全貌は各要素とも、「黄金長方形」で囲われていると言われています。
金閣寺
「金閣寺」は、言わずと知れた日本が誇る名所の1つです。京都市北区にある臨済宗相国寺派のお寺で、「金閣寺」は通称にあたり、正式名称は「鹿苑寺(ろくおんじ)」となります。「金閣寺」の呼び名は、舎利殿「金閣」から来ていますが、現在は正式名称よりもこちらの方が有名となっています。
「金閣寺」もまた、「黄金比」が隠された建物の例の1つです。「金閣寺」を池に面した南側から見ると、その高さと横幅の比率が1:1.618になると言われています。
ミロのヴィーナス
「ミロのヴィーナス」とは、古代ギリシアで制作された大理石の女性像です。詳細は分かっていませんが、ギリシア神話の女神アフロディーテをかたどったものと言われています。作者についても詳しいことは伝わっていないものの、紀元前130年ごろに活躍した、アンティオキアのアレクサンドロスと考えられています。「ミロ」の名は、発見地であるミロス島にちなんでいます。
「ミロのヴィーナス」もまた「黄金比」が隠れた例の1つで、像をへその部分で上下に2分すると、上半身が1で下半身が1.618の比率となります。
名刺
「名刺」は日常でもよく使われるアイテムですが、こうしたものも「黄金比」が使われている事例となっています。名刺の一般的なサイズは、55×91㎜程度です。これを比率で表すと、1:1.654となります。「黄金比」の比率は、前述のように1:1.618ですから、ぴったり同じというわけではありませんが、ほぼ同様の比率となります。
ちなみに欧米の名刺は51×89㎜と、日本のものよりやや小さく、比率も黄金比からはややずれるようになっています。
Apple社のロゴ
「黄金比」の事例の6つ目は、「Apple社のロゴ」です。アップル製品のユーザーでなくとも、日々見かけるほど有名なロゴですが、この中にも「黄金比」が隠されています。「齧りかけの林檎」をかたどったこのロゴは、大小さまざまな曲線から成っていますが、その曲線を分解すると、直径が1、2、3、5、8、13の円で構成されていることが分かります。
これは「フィボナッチ数列」と呼ばれるもので、先述の「黄金長方形」の中の正方形にぴったり当てはまるようになっています。
オードリー・ヘプバーンの顔
昨日はオードリーヘップバーン????????の気分だったからこれ????可愛すぎて同じ人間と思いたくないよ????????おてんばなとこが良き????あと、私なら猫ちゃん????に名演技で賞を授けるね????✨ティファニーの店員さんとのやり取りと雨のシーンが最高だなぁ☺️☔#ティファニーで朝食を#映画好きな人と繋がりたい pic.twitter.com/26Upm6kqwj
— ぷるりんこ (@xxxapcs24) October 24, 2019
オードリー・ヘップバーンは、言わずと知れた、映画史上最も有名なハリウッド女優の1人です。個性的で気品に満ちた美貌で知られていますが、そのオードリー・ヘップバーンの顔もまた、「黄金比」を持った例の1つとされています。
人の顔には大勢を惹きつける魅力をもった例が多くありますが、その程度を測るのが、「美のマスク」と呼ばれる診断モデルです。「黄金比」を用いて作られたこのマスクに、オードリーの顔はぴったり当てはまると言われています。
凱旋門
「凱旋門」とは、本来戦争で勝利を収めた軍人などを、故国に出迎えるために作られた門を指します。発祥は古代ローマにさかのぼり、歴史上さまざまな凱旋門が作られてきましたが、今日単に「凱旋門」という場合には、パリの「エトワール凱旋門」を指すのが一般的です。
この「エトワール凱旋門」も「黄金比」を意識して作られた建造物の例で、中央開口部の高さと全体の高さの比は1:1.697と、「黄金比」に限りなく近いものになっています。
オウムガイの貝殻
「オウムガイ」とは、南太平洋~オーストラリア近海に生息するオウムガイ科の軟体動物です。「生きている化石」と呼ばれるほど古い種で、祖先は4億5000万年前から5億年前に誕生したとされています。「鸚鵡貝」と日本語で「貝」の名がついていますが、本来はタコやイカに近い生き物となっています。
そのオウムガイの「殻」は、前にも述べたように、「黄金比」の代表例としてよく名前が挙がるものです。オウムガイの殻は、中心に向かって螺旋状になっているのですが、先に挙げた「黄金螺旋」と同じパターンの螺旋を描いています。
Googleロゴ
「Google」は、言わずと知れたIT業界の巨人ですが、特に検索エンジンにおいては世界中で圧倒的なシェアを誇っています。そこで検索時自然に目にすることになるのが「Googleロゴ」ですが、こちらのロゴもまた、「黄金比」が隠された例の1つとなっています。
現在のGoogleロゴは、2015年に変更されたデザインで、フォントもフラットでシンプルな形となっています。一目見て円を強調したデザインなのに気づきますが、実は大小2種類の円で構成されており、その2つの円の直径を比べると、1:1.618の黄金比となります。
エジプトのピラミッド
「ピラミッド」とは、エジプトや中南米などの地域に見られる四角錐状の巨石建造物の総称ですが、一般的に「ピラミッド」という場合には、「エジプトのピラミッド」を指して言うことが多くなっています。こちらはエジプト古王国からエジプト中王国時代のファラオか、もしくはその家族の墓に当たるものです。
この「ピラミッド」もまた、「黄金比」が隠れた例の1つになります。「ピラミッド」の高さと一辺の長さの比は、1:1.618となっています。
Twitterのロゴ
「Twitter」は、世界的に人気のソーシャルネットワークサービス(SNS)で、日本でも数多くの利用者がいます。日常的なできごとの投稿はもちろん、非常時の情報ソースとしても利用されるなど、幅広い活用ができるツールとして一般に定着しています。
その「Twitterロゴ」は、おなじみの青い小鳥ですが、こちらのロゴも「黄金比」が隠された例の1つとなっています。やはり曲線で構成されたパーツの円の大きさを比べてみると、「黄金比」の1:1.618となります。
ペプシのロゴ
ペプシのロゴマークがもう頭の悪い人にしか見えないんだけど pic.twitter.com/BP8KWTJ3Gg
— ハル (@_keionharu_) September 15, 2017
「コカ・コーラ」と並んで有名なコーラのブランドが、「ペプシコーラ」です。知名度では「コカ・コーラ」にやや劣るものの、ユニークな商品展開などで存在感を見せ、根強いファンが多数存在します。特に味については、「コカ・コーラよりペプシ」という人も多くなっています。
その「ペプシロゴ」もまた、「黄金比」が隠れた例の1つです。ペプシロゴもいくつもの円で構成されていますが、その円を分解して「黄金長方形」に当てはめると、見事にその中に納まるようになっています。
ミケランジェロのアダム
アダムの創造(The Creation of Adam)
1511年頃 ミケランジェロ pic.twitter.com/oeOHWVrkdI
— ビューティフルライフ (@beau_L18) January 20, 2019
「アダムの創造」は、ルネサンス期の巨匠であるミケランジェロの傑作の1つとして知られる絵画です。ヴァチカンの有名な「システィーナ礼拝堂」の天井に描かれたもので、旧約聖書の「創世記」に取材した絵となっています。
この「アダムの創造」も、「黄金比」を用いて描かれた絵の例です。この絵は神の指とアダムの指が触れ合う場面を描いていますが、その画面構成を長方形で区切ってみると、見事な「黄金長方形」が出来上がります。
クレジットカード・キャッシュカード
クレジットカードやキャッシュカードは、私たちの生活に欠かすことのできないアイテムです。日常で活躍するこうしたものも、「黄金比」が使われている事例の1つとなっています。
クレジットカードやキャッシュカードにはいろいろな種類がありますが、実はサイズはどれも同一です。これには世界的な規格があり、全てそれに沿って作られているためです。その規格では、縦が53.98㎜、横が85.60㎜と、比率が「黄金比」に沿ったものとなっています。
タバコの箱
健康意識の高まりや値上げの影響もあり、喫煙者の数は年々減り続けています。それでもやはりタバコは手放せないという人は大勢いるでしょうが、そのタバコの箱もまた、「黄金比」が使われた事例の1つとなっています。
一口にタバコの箱と言っても、商品によって大きさはさまざまですが、一般的なレギュラサイズは、横が55㎜、縦が88mmとなっています。これを比率で表すと、1:1.6と、「黄金比」に重なるよう作られていることが分かります。
台風
「黄金比」が確認できる形は、人間が作ったものばかりとは限りません。自然現象の中にも、「黄金比」が隠されている例があります。その1つが、「台風」です。
ご存知のように、台風やハリケーンは、外側から中心に向かって渦を巻くような形をしています。天気図でもはっきりと確認できますが、この渦の形が「黄金比」に合うと言われています。実際に先述の「黄金螺旋」と重ねてみると、台風の螺旋とぴったり重なることが多くなっています。
唐招提寺金堂
奈良の名刹「唐招提寺」も、「黄金比」を持つ事例として知られています。唐招提寺は唐の帰化僧である鑑真が、奈良時代に建立したものです。「唐招提寺」の名前は、「唐の律を学ぶ道場」を意味する「唐律招提」に由来しています。
唐招提寺で「黄金比」を用いているのは、南大門をくぐった正面に位置する「金堂」です。「金堂」は寺の本尊を安置する場所ですが、こちらの「唐招提寺金堂」は、縦と横幅の比率が「黄金比」に重なるものとなっています。
富嶽三十六景 神奈川沖浪裏
I think that also it may be better to print to T-shirts as it is.????????
''富嶽三十六景''
Fugakusanjūrokkei
It's very beautiful. pic.twitter.com/d0A9byPfsg— MIZUKI (@mi_z__uKI) October 22, 2019
続いての「黄金比」の事例は、「富嶽三十六景 神奈川沖浪裏(かながわおきなみうら)」です。葛飾北斎の代表作で、世界的にもっとも有名な浮世絵の1つでもあります。「富嶽三十六景」は富士山をさまざまな場所から描いた北斎晩年の連作ですが、「神奈川沖浪裏」はその1つに当たります。
この作品は、左側の大きな波の遠景に富士が見える構図ですが、画面全体を波の大きさに合わせて切り取ると、縦横の比が「黄金比」に重なるようにできています。
竜安寺の石庭
「竜安寺(りょうあんじ)」は、京都市右京区にある臨済宗の妙心寺派のお寺です。開基(創建者)は細川勝元で、釈迦如来を本尊とします。世界遺産にも登録されている名所で、「龍安寺」が正式な名ですが、「竜安寺」と書く場合もあります。
「竜安寺」で特に有名なのが、「石庭」と呼ばれる方丈庭園です。白砂を敷き詰めた中に、大小15の石を配置した庭ですが、この庭はまさしく「黄金長方形」の比率となっており、各石もその対角線上に位置しています。
iPod
Appleロゴの曲線が「黄金比」にぴったり重なるのは前述の通りですが、Apple社にはそれ以外にも、「黄金比」を利用したデザインが多くあります。その1つの例が、「iPod」です。「iPod」は携帯型デジタル音楽プレーヤーの先駆けとなった製品で、現在でも多くのユーザーを持っていますが、そのデザインにも「黄金比」が隠されています。
こちらの「黄金比」はもちろん縦横の比率で、単純にそのままのものもあれば、いくつかの「黄金長方形」を組み合わせてできているものもあります。
トランプ
先ほどのクレジットカードやキャッシュカードの例でもわかるように、カードの類には「黄金比」を用いたものが多くなっています。その1つとして挙げられるのが、「トランプ」です。言わずもがなのカードゲームの代表格ですが、このサイズもまた、「黄金比」に沿ったものとなっています。
標準的なトランプのサイズは2種類ありますが、そのうち「ブリッジサイズ」と呼ばれるものは、「黄金比」に近い比率となっています。ちなみにもう1つの「ポーカーサイズ」の比率は、やはり「貴金属比」の一種である「白銀比」とほぼ同じです。
パソコンのワイドモニター
続いて紹介する「黄金比」の事例は、「パソコンのワイドモニター」です。モニターには主に「スクエアモニター」と「ワイドモニター」の2種類がありますが、このうちワイドモニターのアスペクト比は、「黄金比」に関連したものとなっています。「アスペクト比」とは矩形(長方形)の長辺と短辺の比率のことで、ワイドモニターの比率は16:10と、「黄金比」とほぼ同じものとなっています。ただ、現在は人間の視野に適した16:9のものが主流となりつつあります。
ひまわりの種
上の項において、人工物だけでなく自然界の中にも「黄金比」の例が見つかると述べましたが、その1つが「ひまわりの種」です。
ひまわりと言えば、黄色い花びらに囲まれるように多くの種が並んでいる姿が思い浮かびますが、「黄金比」が隠れているのは、この種の並び方です。よく見てみると、これらの種は、時計周りと反時計回りの2種類の螺旋を描いていることがわかります。この2つの螺旋の数の組み合わせにはパターンがあり、その組み合わせの数を比率にしてみると、「黄金比」に沿うことが明らかとなっています。
正五角形
最後に紹介する「黄金比」の例は、「正五角形」です。「ペンタゴン」とも呼ばれ、対角線をつなぐと「五芒星」になることでも知られる多角形ですが、この中にも「黄金比」が隠されています。
正五角形には、次のような定理があります。すなわち、「1辺の長さが1の正五角形の対角線の長さは、(1+√5/2)である」というものです。つまり、正五角形の辺と対角線の比率は1:(1+√5)/2となるわけで、これは先に説明した「黄金比」の式そのものにあたります。

この記事が気に入ったら いいね!しよう



























